Spiral Review Write the Equation of a Parabloa With a Directrix Ofy=-5 and a Vertex of (00)

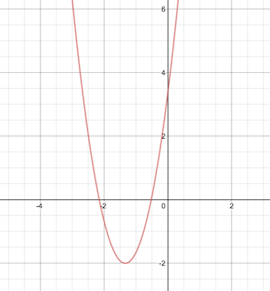
Once y'all accept the quadratic formula and the basics of quadratic equations downwardly cold, information technology'southward fourth dimension for the next level of your relationship with parabolas: learning near their vertex course.

Read on to learn more nearly the parabola vertex form and how to convert a quadratic equation from standard grade to vertex form.

feature image credit: SBA73/Flickr

Why Is Vertex Form Useful? An Overview

The vertex form of an equation is an alternate way of writing out the equation of a parabola.

Ordinarily, y'all'll come across a quadratic equation written as $ax^2+bx+c$, which, when graphed, will be a parabola. From this course, it'south easy plenty to find the roots of the equation (where the parabola hits the $x$-axis) by setting the equation equal to cypher (or using the quadratic formula).

If you demand to find the vertex of a parabola, however, the standard quadratic form is much less helpful. Instead, you'll want to convert your quadratic equation into vertex grade.

What Is Vertex Form?

While the standard quadratic form is $ax^2+bx+c=y$, the vertex form of a quadratic equation is $\bi y=\bi a(\bi x-\bi h)^two+ \bi m$.

In both forms, $y$ is the $y$-coordinate, $x$ is the $x$-coordinate, and $a$ is the constant that tells you whether the parabola is facing upwards ($+a$) or down ($-a$). (I recollect about information technology equally if the parabola was a bowl of absurdity; if there's a $+a$, I can add applesauce to the basin; if there's a $-a$, I can shake the absurdity out of the bowl.)

The difference between a parabola's standard class and vertex grade is that the vertex grade of the equation too gives you lot the parabola's vertex: $(h,k)$.

For case, take a look at this fine parabola, $y=3(x+iv/3)^2-2$:

Based on the graph, the parabola'south vertex looks to be something like (-1.v,-2), simply it's hard to tell exactly where the vertex is from just the graph alone. Fortunately, based on the equation $y=three(x+4/3)^2-2$, nosotros know the vertex of this parabola is $(-4/3,-two)$.

Why is the vertex $(-iv/iii,-ii)$ and not $(4/3,-2)$ (other than the graph, which makes it clear both the $ten$- and $y$-coordinates of the vertex are negative)?

Remember: in the vertex class equation, $h$ is subtracted and $k$ is added. If you lot accept a negative $h$ or a negative $one thousand$, you'll need to make sure that you subtract the negative $h$ and add the negative $k$.

In this case, this means:

$y=iii(x+iv/3)^two-2=iii(x-(-4/iii))^two+(-2)$

then the vertex is $(-four/three,-2)$.

You should e'er double-check your positive and negative signs when writing out a parabola in vertex course, particularly if the vertex does not have positive $x$ and $y$ values (or for yous quadrant-heads out there, if it's not in quadrant I). This is similar to the check y'all'd practise if you lot were solving the quadratic formula ($x={-b±√{b^two-4ac}}/{2a}$) and needed to make certain y'all kept your positive and negatives straight for your $a$due south, $b$s, and $c$s.

Beneath is a table with farther examples of a few other parabola vertex class equations, along with their vertices. Note in item the difference in the $(ten-h)^2$ part of the parabola vertex form equation when the $x$ coordinate of the vertex is negative.

Parabola Vertex Form	Vertex Coordinates
$y=v(10-4)^2+17$	$(four,17)$
$y=2/3(ten-8)^2-ane/iii$	$(8,-1/3)$
$y=144(ten+1/2)^2-two$	$(-1/two,-2)$
$y=one.8(x+two.four)^ii+two.4$	$(-ii.iv,2.four)$

How to Convert From Standard Quadratic Form to Vertex Grade

Most of the time when you lot're asked to convert quadratic equations between different forms, you'll be going from standard form ($ax^2+bx+c$) to vertex class ($a(x-h)^2+k$).

The procedure of converting your equation from standard quadratic to vertex form involves doing a set of steps called completing the square. (For more than about completing the foursquare, be sure to read this article.)

Let'southward walk through an example of converting an equation from standard form to vertex form. We'll offset with the equation $y=7x^2+42x-iii/14$.

The first thing you lot'll desire to practise is move the abiding, or the term without an $10$ or $ten^2$ next to it. In this case, our constant is $-3/fourteen$. (We know it's negative $3/14$ considering the standard quadratic equation is $ax^two+bx+c$, not $ax^two+bx-c$.)

First, nosotros'll take that $-3/xiv$ and move it over to the left side of the equation:

$y+three/14=7x^2+42x$

The next step is to factor out the vii (the $a$ value in the equation) from the right side, like so:

$y+3/14=7(x^ii+6x)$

Slap-up! This equation is looking much more than similar vertex form, $y=a(x-h)^2+one thousand$.

At this point, you might be thinking, "All I need to practice at present is to move the $3/14$ back over to the right side of the equation, correct?" Alas, non so fast.

If yous take a await at part of the equation inside of the parentheses, you'll discover a problem: it'southward non in the grade of $(ten-h)^two$. There are too many $10$s! And then we're non quite done all the same.

What we need to do now is the hardest part—completing the square.

Let's have a closer expect at the $x^2+6x$ role of the equation. In order to factor $(ten^ii+6x)$ into something resembling $(x-h)^2$, we're going to demand to add a constant to the inside of the parentheses—and we're going to need to remember to add that constant to the other side of the equation as well (since the equation needs to stay balanced).

To set this upwards (and make certain we don't forget to add the abiding to the other side of the equation), we're going to create a bare infinite where the abiding will go along either side of the equation:

$y+3/14+7($   $)=7(x^2+6x+$   $)$

Annotation that on the left side of equation, nosotros made sure to include our $a$ value, seven, in front of the infinite where our constant will go; this is because we're not simply adding the constant to the right side of the equation, simply we're multiplying the constant past whatever is on the outside of the parentheses. (If your $a$ value is 1, you don't demand to worry about this.)

The side by side step is to consummate the square. In this instance, the square you lot're completing is the equation inside of the parentheses—by adding a abiding, you're turning it into an equation that tin can be written every bit a square.

To calculate that new constant, take the value next to $x$ (half-dozen, in this case), divide information technology by 2, and square information technology.

$(half dozen/2)^two=(3)^2=ix$. The constant is nine.

The reason we halve the 6 and square it is that nosotros know that in an equation in the class $(x+p)(ten+p)$ (which is what we're trying to get to), $px+px=6x$, so $p=6/2$; to get the constant $p^ii$, we thus have to take $half dozen/ii$ (our $p$) and square it.

Now, replace the bare space on either side of our equation with the abiding ix:

$y+3/14+seven(nine)=7(x^2+6x+nine)$

$y+{3/14}+63=seven(10^ii+6x+9)$

$y+{3/14}+{882/14}=7(10^2+6x+nine)$

$y+{885/fourteen}=7(x^2+6x+nine)$

Next, cistron the equation inside of the parentheses. Because we completed the square, you will be able to factor it as $(x+{\some \number})^ii$.

$y+{885/fourteen}=7(x+iii)^ii$

Last step: motility the non-$y$ value from the left side of the equation back over to the correct side:

$y=7(ten+iii)^two-{885/14}$

Congratulations! Yous've successfully converted your equation from standard quadratic to vertex form.

Now, most issues won't just inquire y'all to catechumen your equations from standard class to vertex form; they'll want you to actually give the coordinates of the vertex of the parabola.

To avoid getting tricked by sign changes, permit'south write out the full general vertex form equation direct above the vertex form equation we but calculated:

$y=a(10-h)^2+k$

$y=seven(x+three)^2-{885/14}$

And then we tin can easily find $h$ and $thou$:

$-h=three$

$h=-3$

$+k=-{885/14}$

The vertex of this parabola is at coordinates $(-three,-{885/14})$.

Whew, that was a lot of shuffling numbers around! Fortunately, converting equations in the other management (from vertex to standard form) is a lot simpler.

How to Convert From Vertex Form to Standard Form

Converting equations from their vertex form to the regular quadratic grade is a much more straightforward procedure: all you need to do is multiply out the vertex form.

Let's take our example equation from earlier, $y=3(10+4/iii)^two-2$. To turn this into standard form, we merely aggrandize out the right side of the equation:

$$y=iii(10+4/3)^ii-2$$

$$y=3(10+iv/3)(x+4/3)-2$$

$$y=3(10^2+{eight/3}x+16/9)-2$$

$$y=3x^2+8x+{16/3}-two$$

$$y=3x^2+8x+{16/iii}-{6/three}$$

$$y=3x^2+8x+x/3$$

Tada! Y'all've successfully converted $y=3(10+4/3)^ii-2$ to its $ax^2+bx+c$ form.

Parabola Vertex Class Practise: Sample Questions

To wrap upwards this exploration of vertex course, we accept four instance problems and explanations. See if you tin can solve the problems yourself before reading through the explanations!

#1: What is the vertex form of the quadratic equation $x^2+ 2.6x+1.2$?

#2: Convert the equation $7y=91x^ii-112$ into vertex course. What is the vertex?

#3: Given the equation $y=2(10-iii/two)^2-ix$, what are the $x$-coordinates of where this equation intersects with the $x$-axis?

#4: Find the vertex of the parabola $y=({1/9}10-six)(x+four)$.

Parabola Vertex Form Do: Solutions

#1: What is the vertex grade of the quadratic equation ${\bi x^2}+ 2.half-dozen\bi x+1.2$?

Start past separating out the non-$x$ variable onto the other side of the equation:

$y-1.ii=x^ii+2.6x$

Since our $a$ (as in $ax^2+bx+c$) in the original equation is equal to 1, nosotros don't need to cistron it out of the right side hither (although if you lot want, you can write $y-1.2=1(x^2+2.6x)$).

Next, divide the $ten$ coefficient (2.half-dozen) by 2 and square it, then add the resulting number to both sides of the equation:

$(2.half-dozen/2)^two=(1.3)^ii=1.69$

$y-1.2+ane(1.69)=1(ten^2+two.6x+1.69)$

Gene the right side of the equation inside the parentheses:

$y-1.ii+1.69=(10+1.iii)^two$

Finally, combine the constants on the left side of the equation, then motility them over to the right side.

$y-ane.2+1.69=(x+one.iii)^2$

$y+0.49=(x+1.3)^2$

Our answer is $y=(x+1.iii)^ii-0.49$.

#ii: Convert the equation $vii\bi y=91\bi ten^2-112$ into vertex form. What is the vertex?

When converting an equation into vertex grade, y'all want the $y$ have a coefficient of 1, and then the offset thing we're going to do is divide both sides of this equation past seven:

$7y= 91x^2-112$

${7y}/7= {91x^two}/7-112/7$

$y=13x^ii-sixteen$

Next, bring the constant over to the left side of the equation:

$y+16=13x^2$

Factor out the coefficient of the $x^2$ number (the $a$) from the right side of the equation

$y+xvi=13(x^2)$

Now, normally you lot'd have to complete the foursquare on the right side of the equation inside of the parentheses. However, $x^2$ is already a square, then y'all don't need to practice anything too moving the constant from the left side of the equation back to the correct side:

$y=thirteen(10^2)-16$.

Now to find the vertex:

$y=a(x-h)^two+k$

$y=13(x^2)-16$

$-h=0$, then $h=0$

$+one thousand=-xvi$, then $k=-sixteen$

The vertex of the parabola is at $(0, -16)$.

#three: Given the equation $\bi y=2(\bi 10-3/ii)^two-9$, what is(are) the $\bi 10$-coordinate(s) of where this equation intersects with the $\bi x$-axis?

Because the question is asking you to detect the $x$-intercept(southward) of the equation, the first footstep is to fix $y=0$.

$y=0=two(10-iii/2)^2-9$.

Now, in that location are a couple of ways to go from here. The sneaky way is to utilise the fact that there's already a square written into the vertex class equation to our advantage.

First, we'll motility the constant over to the left side of the equation:

$0=2(ten-3/2)^2-ix$

$9=2(x-three/2)^2$

Next, we'll separate both sides of the equation by 2:

$9/2=(x-iii/two)^2$

Now, the sneaky role. Take the square root of both sides of the equation:

$√(9/2)=√{(x-3/2)^2}$

$±three/{√2}=(ten-3/2)$

$±{{three√2}/2}=x-{3/2}$

${3√2}/2=ten-{3/ii}$ and ${-iii√ii}/2=x-{three/ii}$

$x=3/2+{three√2}/two$ and $10=three/2-{iii√2}/2$

Alternatively, you lot can find the roots of the equation by first converting the equation from vertex course back to the standard quadratic equation grade, then using the quadratic formula to solve information technology.

First, multiply out the correct side of the equation:

$0=two(x-{3/2})^2-nine$

$0=ii(ten^ii-{6/ii}x+{9/4})-9$

$0=2x^two-6x+{9/two}-9$

Then, combine like terms:

$0=2x^2-6x-9/two$

At this point you lot can either cull to try and work out the factoring yourself by trial and error or plug the equation into the quadratic formula. If I see a coefficient next to the $x^2$, I usually default to the quadratic formula, rather than trying to keep everything straight in my head, so permit'due south go through that hither.

Remembering that $2x^two-6x-9/2$ is in the course of $ax^2+bx+c$:

$x={-b±√{b^2-4ac}}/{2a}$

$x={-(-half-dozen)±√{(-vi)^2-4(2)(-9/two)}}/{ii(ii)}$

$x={half dozen±√{36-4(-9)}}/4$

$10={6±√{36+36}}/4$

$x={6±√{72}}/four$

$x={half-dozen+6√2}/4$ and $x={-6-half-dozen√2}/four$

$x=iii/two+{3√2}/2$ and $x=3/2-{iii√2}/2$

#4: Find the vertex of the parabola $\bi y=({i/9}\bi x-6)(\bi x+4)$.

The first step is to multiply out $y=({ane/9}x-half dozen)(x+4)$ so that the abiding is split from the $10$ and $x^2$ terms.

$y={one/ix}{x^ii}+(-half dozen+{4/nine})x-24$

Next, move the constant over to the left side of the equation.

$y+24={1/9}{ten^two}-{50/ix}x$

Cistron out the $a$ value from the correct side of the equation:

$y+24={i/9}(x^two-50x)$

Create a space on each side of the equation where you'll exist adding the abiding to complete the square:

$y+24+1/nine($   $ )={1/9}(x^2-50x+$   $)$

Calculate the constant by dividing the coefficient of the $x$ term in half, then squaring it:

$(-50/2)^2=(-25)^2=625$

Insert the calculated constant back into the equation on both sides to consummate the foursquare:

$y+24+{1/9}(625)={1/nine}(x^ii-50x+625)$

Combine similar terms on the left side of the equation and factor the right side of the equation in parentheses:

$y+{216/9}+{625/nine}={1/9}(ten-25)^2$

$y+{841/9}={one/9}(ten-25)^2$

Bring the abiding on the left side of the equation back over to the right side:

$y={1/nine}(ten-25)^2-{841/nine}$

The equation is in vertex class, woohoo! Now, to find the vertex of the parabola:

$y=a(x-h)^2+m$

$y={i/9}(x-25)^2-{841/9}$

$-h=-25$ then $h=25$

$+k=-{841/9}≈-93.four$ (rounded)

The vertex of the parabola is at $(25,-93.iv)$.

What's Next?

Can't become enough of completing the square? Review how to complete the square and when else you lot might desire to use information technology in this article.

While graphing parabolas is fun to do by hand, a graphing estimator is still a handy tool to have. Read our article on the best graphing calculators (both physical and online) hither.

In the midst of coordinate geometry and factoring quadratics? Our list of perfect squares and graph quadrant definitions are here for you.

Studying for Saturday/Human action Math? Our articles on the critical math formulas you need to know for Sat Math and Deed Math are indispensable.

Have friends who also need help with test prep? Share this article!

About the Author

Laura graduated magna cum laude from Wellesley College with a BA in Music and Psychology, and earned a Master's degree in Limerick from the Longy Schoolhouse of Music of Bard College. She scored 99 percentile scores on the Sat and GRE and loves advising students on how to excel in loftier schoolhouse.

ousleyqueent.blogspot.com

Source: https://blog.prepscholar.com/vertex-form-parabola

Share this post